Convex Sets and Polynomials

A Primer on Convex Sets

For convex shapes, if two points are present inside the shape, every point lying on the line connecting the two points will also be contained in the shape. As opposed to concave shapes that do not have this property.

Convex Sets are similarly sets of vectors that contains every vector on the straight line between them.

Thus any vector $X=A+\theta (B-A)$, where $0\le \theta \le 1$, lies on the line between $A$ and $B$. This definition is inclusive of both the generator vectors $A$ and $B$, meaning the convex shape described includes the boundaries without any holes. More concretely, a Convex Set $C$ is a set where $\theta x_1+(\theta -1)x_2\in C,\forall \theta [0,1]$ and $x_1,x_2\in C$.

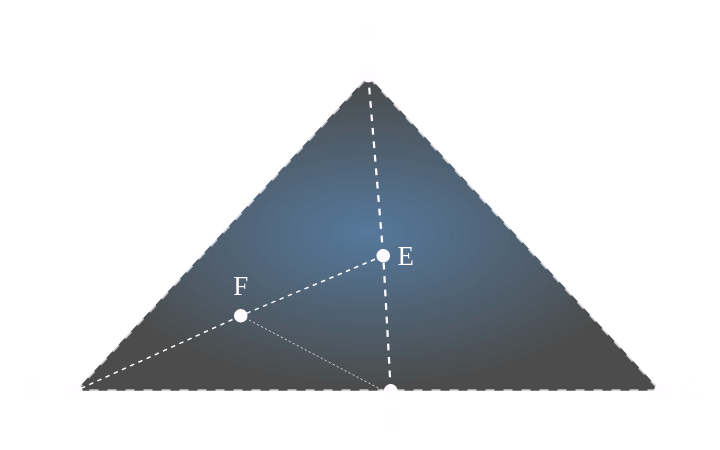
A convex set does not have any holes in it as it can be recursively filled. In the above example; $A$, $B$ and $C$ are the generator vectors. Thus the vector $D$ must also be in the set as it falls on the straight line between $B$ and $C$. Following which we can say that since $E$ falls on the line between $A$ and $D$, it must also be contained in the set. Thus, we can claim that any point $X$ present in the interior of the region described must be contained by the set.

Set of all $n$-polynomials is Convex

The set of all $n$th degree polynomials has the following structure:

$$\left\{P(x)\mid P(x)=\sum _{i=0}^n{a}_i{x}^i\forall n\in {\mathbb{N}}_0\right\}$$

This includes polynomials of every degree imaginable, provide your imagination only considers only the natural numbers, sans zero. Is this resulting infinite set of polynomials a convex set?

Yes.

Every convex set $C$ has a defining property: $\theta x_1+(1-\theta )x_2\in C$ for two elements $x_1,x_2\in C$ and $0\le \theta \le 1$. This requires that the sets to contain elements that can be found “in-between” the two generator elements $x_1$ and $x_2$.

Keeping this in mind, we consider two polynomials of $n$-th degree; $H(x)$ and $G(x)$.

Respectively:

$$H(x)=h_0+h_{1}x+h_2{x}^2+\cdots +h_n{x}^n$$ $$G(x)=g_0+g_{1}x+g_2{x}^2+\cdots +g_n{x}^n$$

Adding both, we have:

$$\begin{array}{rl}& \theta G(x)+(1-\theta )H(x)=\theta g_0+(1-\theta )h_0+\theta g_{1}x+(1-\theta )h_{1}x+\theta g_2{x}^2+(1-\theta )h_2{x}^2+\cdots +\theta g_n{x}^n+(1-\theta )h_n{x}^n\\ & \theta G(x)+(1-\theta )H(x)=(\theta g_0+(1-\theta )h_0)+(\theta g_1+(1-\theta )h_1)x+(\theta g_2+(1-\theta )h_2)x^2+\cdots +(\theta g_n+(1-\theta )h_n)x^n\\ & K(x)=\theta G(x)+(1-\theta )H(x)=\underset{k_0}{\underbrace{(\theta g_0+(1-\theta )h_0)}}+\underset{k_1}{\underbrace{(\theta g_1+(1-\theta )h_1)}}x+\underset{k_2}{\underbrace{(\theta g_2+(1-\theta )h_2)}}{x}^2+\cdots +\underset{k_n}{\underbrace{(\theta g_n+(1-\theta )h_n)}}{x}^n\end{array}$$

By restructuring the resultant polynomial, we have:

$$K(x)=k_0+k_{1}x+k_2{x}^2+\cdots +k_n{x}^n$$

which is our new $n$-polynomial.