The Basics (?)

Info

Consider a set $S=\{1,2,3\}$

$x_S$ is some subset of the set $S$, the complement of this subset can be demonstrated as $x_{-S}$.

$$\begin{array}{c}\mathsf{D}=\alpha \mathsf{B}+c⟹D_{i,j}=\alpha B_{i,j}+c\end{array}$$

Broadcasting:

$$\begin{array}{c}\mathsf{D}=\mathsf{A}+b⟹D_{i,j}=A_{i,j}+b_j\end{array}$$

Elements of $b$ are added to each row of the matrix $\mathsf{D}$.

Since dot product gives a scalar it is a commutative operation in the following way: $x^{\top }y=(x^{\top }y{)}^{\top }=y^{\top }x$

Matrix Multiplication

$$\begin{array}{c}\mathsf{C}=\mathsf{AB}\\ C_{i,j}=\sum _k{A}_{i,k}{B}_{k,j}\end{array}$$

(each element in the matrix $\mathsf{C}$ is calculated via a dot product of $i$th row of $\mathsf{A}$ and $j$th column of $\mathsf{B}$.)

If $x$ and $y$ are solutions to $\mathsf{Ax}=\mathsf{b}$, then $z=\alpha x+(1-\alpha )y$ is also a solution for any $\alpha \in \mathbb{R}$.

Info

A visualization for $\mathsf{Ax}=\mathsf{b}$ can be seen as:

$x_1$ determines how much to go in $A_{:,1}$ direction.

Therefore for each element of the resulting vector we will have $\mathsf{A}x={\sum }_i{x}_i{A}_{:,i}$, where $x_i{A}_{:,i}$ is a scalar multiplication of $x_i$ and all elements of the $A_{:,i}$ column vector.

The vector-matrix multiplication operation can be translated into a linear combination of the column vectors of the original matrix, multiplied with each element of the vector column:

$$\alpha A_{:,1}+\beta A_{:,2}+\gamma A_{:,3}$$

From the above, we see that $\mathsf{b}$ will be a solution of $\mathsf{Ax}=\mathsf{b}$ only when it is in the column span (range) of $\mathsf{A}$.

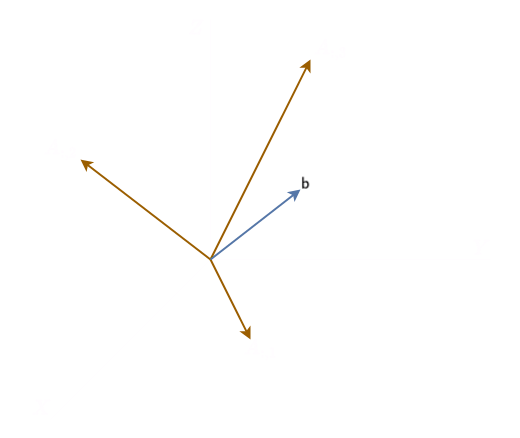
$\mathsf{b}$ can be thought of as being pulled $x_1$ quantity in $A_{:,1}$ direction $x_2$ times in $A_{:,2}$ direction and $x_3$ times in $A_{:,3})$ direction. We need $\mathsf{A}$ to have at least $m$ independent columns in order to define ${\mathbb{R}}^m$ as their column space ($n\ge m$).

if $\mathsf{A}$ is a $3\times 2$ matrix and $\mathsf{b}$ is $3\times 1$, $x$ is 2-dimensional, so $x$ defines only a 2-D plane within ${\mathbb{R}}^3$, the equation has a solution iff $\mathsf{b}$ lies on that plane.

flowchart TD

a["conditions"] --> b["have to at least describe m-dimensions"] & c["m-vectors should be linearly independent"]
b --> c

$x={\mathsf{A}}^{-1}\mathsf{b}$ : at most one solution for each value of $\mathsf{b}$

If overdetermined ($n\ge m$), there is more than one way to parameterize the solution.

Any Norm function will be of the following form: $f:V\to \mathbb{R}$

Note

Norm are generally a way of measuring distance which scales from scalar multiplication.

$L^0$ norm which corresponds to the number of non-zero entries in a vector is not a valid distance metric as scaling the vector by $\alpha$ does not change the number of non-zero entries.

Infinity Norm:

$$\begin{array}{c}\Vert x{\Vert }_{\infty }=\underset{i}{\max }|x_i|\end{array}$$

This norm measures the maximum discrepancy between two elements in a vector.

Frobenius Norm:

$$\begin{array}{c}\Vert \mathsf{A}{\Vert }_F=\sqrt{\sum _{i,j}{A}_{i,j}^2}\end{array}$$

Frobenius Norm is considered w.r.t a matrix, for vectors (or single column matrices) this will be equivalent to the $L^2$ norm of the vector.

Vectors having $\Vert \cdot {\Vert }_2=1$ and $x^{\top }y=0$ are called orthonormal vectors.

Diagonal Matrices: Diagonal Matrices have only diagonal elements, rest are all zeroes.

$$\text{diag}(v)=\left(\begin{array}{cccc}{v}_1& 0& 0& \dots \\ 0& v_2& 0& \dots \\ 0& 0& v_3& \dots \\ ⋮& ⋮& ⋮& \ddots \end{array}\right)$$ $$\text{diag}(v{)}^{-1}=\text{diag}\left({\left[\frac{1}{v_1},\dots ,\frac{1}{v_n}\right]}^{\top }\right)$$ $$\text{diag}(v)x=v\odot x$$ $$\underset{\text{diagonal}}{\underbrace{\mathsf{D}}}x$$

For a non-square tall diagonal matrix zeroes are added to the end of the matrix. For a wide matrix, elements of $x$ are dropped during multiplication.

Symmetric Matrices: $\mathsf{A}={\mathsf{A}}^{\top }$

Singular Matrices: Square matrices with linearly dependent columns.

Orthogonal Matrices: rows (columns) mutually orthonormal

$$\begin{array}{c}{\mathsf{A}}^{\top }\mathsf{A}=\mathsf{A}{\mathsf{A}}^{\top }=I\\ {\mathsf{A}}^{-1}={\mathsf{A}}^{\top }\end{array}$$

Eigenvectors and Eigenvalues

$$\mathsf{A}v=\underset{\text{eigenvalue}}{\underbrace{\lambda }}\stackrel{eigenvector}{\overbrace{v}}$$ $$v^{\top }\mathsf{A}=v^{\top }\lambda :\text{ right eigenvector \& eigenvalue}$$ $$\mathsf{A}(sv)=\lambda (sv),\forall s\in \mathbb{R},s\ne o$$ $$\begin{array}{c}\mathsf{A}v=\lambda v\text{ and }\mathsf{A}u=\lambda u\\ \mathsf{A}v+\mathsf{A}u=\lambda v+\lambda u\\ \mathsf{A}(v+u)=\lambda (v+u)\\ ⟹\mathsf{A}(\alpha v+\beta u)=\lambda (\alpha v+\beta u)\end{array}$$

Matrix $\mathsf{A}$ has $n$ linearly independent eigenvectors $\{v^{(1)},\dots ,v^{(n)}\}$ and corresponding eigenvalues $\{{\lambda }_1,\dots ,{\lambda }_n\}$.

Concatenating the vectors (one vector per column):

$$\begin{array}{c}V=\left[v^{(1)},v^{(2)},\dots ,v^{(n)}\right]\\ \lambda =[{\lambda }_1,{\lambda }_2,\dots ,{\lambda }_n{]}^{\top }\end{array}$$

Eigendecomposition:

$$\begin{array}{c}\mathsf{A}=V\text{diag}(\lambda )V^{-1}\end{array}$$

For any Real Symmetric Matrix we have:

$$\begin{array}{c}\mathsf{A}=Q\Lambda Q^{\top }\end{array}$$

where $Q$ is the diagonal matrix of eigenvalues and $Q^{\top }$ is orthogonal matrix of eigenvalues of $\mathsf{A}$. Eigendecomposition is guaranteed for real symmetric matrices, but they might not unique.

${\Lambda }_{i,i}$ is eigenvalue related to $i$th column of $Q$ ( $Q_{:,i}$ ), since it’s orthogonal (independent basis) we can think of $\mathsf{A}$ as scaling space by ${\lambda }_i$ in direction $v^{(i)}$ . If ${\lambda }_i=0$, matrix is singular.

$$\begin{array}{rlr}& \mathsf{A}=Q\Lambda Q^{\top }& \\ & Q^{\top }\mathsf{A}Q=\Lambda & \\ & x^{\top }\mathsf{A}x=f(x)& s.t.\Vert x{\Vert }_2=1\\ & v_1^{\top }\mathsf{A}{v}_1={\lambda }_1& \end{array}$$

where ${\lambda }_1$ is eigenvalue corresponding to the specific eigenvectors.

$x^{\top }\mathsf{A}x=0⟹x=0$ : A matrix whose eigenvalues are all positive : positive definite

$\forall x,x^{\top }\mathsf{A}x\ge 0$ : A matrix whose eigenvalues are all positive or zero : positive semidefinite

A matrix whose eigenvalues are all negative : negative definite

A matrix whose eigenvalues are all negative or zero : negative semidefinite